[백준 / Java] 1260번 DFS와 BFS

사용한 알고리즘(DFS (재귀, 스택)), (BFS (큐))
DFS
https://cobi-98.tistory.com/30
[필수 알고리즘] DFS 깊이 우선 탐색 (Stack 구조) 이해
DFS 깊이 우선 탐색 (Depth-First Search) 깊이 우선 탐색 (DFS)는 하나의 순환 알고리즘으로 백트래킹에 사용하는 대표적인 탐색 알고리즘이다. 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분
cobi-98.tistory.com
BFS
https://cobi-98.tistory.com/36
[필수 알고리즘] BFS 너비 우선 탐색 (Queue 구조) 이해
BFS 너비 우선 탐색 (Breadth-First Search) 너비 우선 탐색(Breadth-first search, BFS)은 맹목적 탐색방법의 하나로 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색한다. 그렇게 되
cobi-98.tistory.com
🔒 1260번 DFS와 BFS
✔ 문제 설명

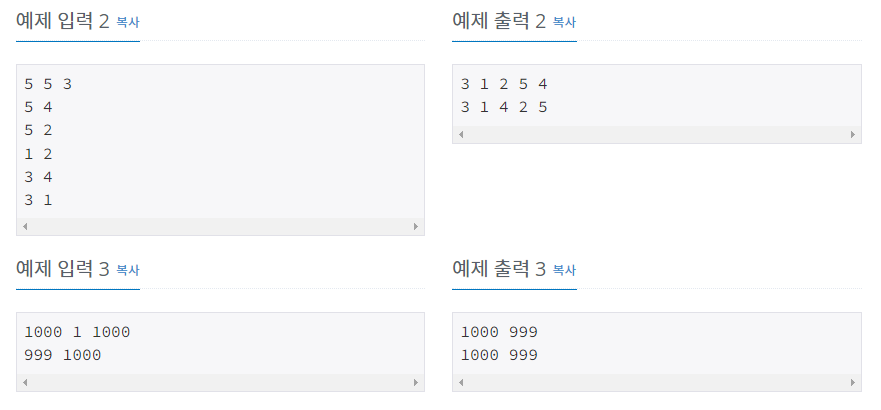
🚩 요구사항 분석
- 시작 정점 이후 번호가 작은 것부터 방문한다.
- 방문을 확인하기위해 boolean [] 변수 사용
- 두 정점 사이에 여러개의 간선이 있을 수 있다.
- 입력으로 주어지는 간선은 양방향이다.
🔑 문제풀이
해당 문제는 DFS 와 BFS의 기본이 되는 문제라고 할 수 있다.
DFS는 재귀, 스택 두 개를 사용하였고,
BFS는 Queue를 사용하였습니다.
DFS : 간선이 있고(map[][] ==1) 방문하지 않았다면(boolean [] false) dfs를 호출해 나가는 구조이다.
BFS : 큐의 처음 삽입한 노드를 빼주고 그 노드와 연결되어있는 (ARR 배열) 노드들을 탐색하여 Queue에 넣는다.
이러한 큐를 반복해서 꺼내 주다가 큐가 비어지면 while문에서 나오는 구조이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main{
public static int vertex;
public static int trunk;
public static int start;
public static int map[][] ;
public static boolean[] visit;
static Queue<Integer> q = new LinkedList<>();
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
vertex = Integer.parseInt(st.nextToken());
trunk = Integer.parseInt(st.nextToken());
start = Integer.parseInt(st.nextToken());
map = new int[vertex+1][vertex+1];
visit = new boolean[vertex+1];
for (int i = 0; i < trunk; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
map[a][b] = map[b][a] = 1;
}
dfs(start);
sb.append('\n');
visit = new boolean[vertex+1];
bfs(start);
System.out.println(sb);
}
// 재귀
// public static void dfs(int start) {
//
// visit[start] = true;
// sb.append(start + " ");
//
// for(int i = 0 ; i <= vertex ; i++) {
// if(map[start][i] == 1 && !visit[i])
// dfs(i);
// }
// }
// 스택
public static void dfs(int start) {
visit[start] = true;
sb.append(start + " ");
for(int i = 0 ; i <= vertex ; i++) {
if(map[start][i] == 1 && !visit[i])
dfs(i);
}
}
public static void bfs(int start) {
q.add(start);
visit[start] = true;
while(!q.isEmpty()) {
start = q.poll();
sb.append(start + " ");
for(int i = 1 ; i <= vertex ; i++) {
if(map[start][i] == 1 && !visit[i]) {
q.add(i);
visit[i] = true;
}
}
}
}
}해당 문제에서 DFS는 재귀호출과 스택 두가지 방법으로 풀어보았다.

메모리와 시간에서 크게 차이가 안 나는 모습이라 스택, 재귀 하나를 외워서 풀이를 진행할 필요 없다.
일반적으로 재귀를 사용하여 구현하지만, 단순한 스택 배열로 구현하기도 하기 때문이다.
그렇기에 알고리즘 구현에있어서 둘 다 알아두면 생각의 범위가 넓어져 더욱 성장할 것이다!!