다익스트라 알고리즘(Dijkstra Algorithm)
다익스트라 알고리즘은 음의 가중치(음의 간선, 음의 값)가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단거리를 구하는 알고리즘을 말한다.
다익스트라 알고리즘은 두 꼭짓점 간의 가장 짧은 경로를 찾는 알고리즘이지만,
더 일반적인 변형은 한 꼭짓점을 "소스" 꼭짓점으로 고정하고 그래프의 다른 모든 꼭짓점까지의 최단경로를 찾는 알고리즘으로 최단 경로 트리를 만드는 것으로도 사용한다.
다익스트라 알고리즘은 그리디 알고리즘이자 다이나믹 프로그래밍 기법을 사용한 알고리즘이라고 볼 수 있다.
그리디 알고리즘과 다이나믹 프로그래밍 기법은 아래의 글에 포스팅되어있다.
그리디 알고리즘
https://cobi-98.tistory.com/44
[필수 알고리즘] 그리디 알고리즘(Greedy Algorithm) 이해
그리디 알고리즘 그리디 알고리즘(욕심쟁이 알고리즘, Greedy Algorithm)이란, "매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하자"라는 모토를 가지는 알고리즘 설계 기
cobi-98.tistory.com
다이나믹 프로그래밍 기법
https://cobi-98.tistory.com/42
[필수 알고리즘] 동적계획법 DP (Dynamic Programming) 이해
동적계획법 DP (Dynamic Programming) 동적 계획법은 프로그래밍 대회 문제에 자주 출현하는 알고리즘 기법 중 하나이며, 프로그램이 실행되는 도중, 실행에 필요한 메모리를 기억하여 할당하는 기법
cobi-98.tistory.com
다익스트라 알고리즘의 메커니즘은 기본적으로
아래 두 단계를 반복하여 임의의 노드에서 각 모든 노드까지의 최단거리를 구하는 문제에서 활용할 수 있다.
임의의 노드에서 다른 노드로 가는 값을 비용이라고 한다.
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다(그리디 알고리즘)
- 해당 노드로부터 갈 수 있는 노드들의 비용을 갱신한다(다이나믹 프로그래밍)
가능한 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 대부분의 문제에 응용되며, 적용하는 문제를 그림으로 살펴보며 이해해 보자.
다익스트라 알고리즘 그림 설명
A노드에서 출발하여 F노드로 가는 최단 경로를 구하는 문제를 다익스트라 알고리즘을 활용한다.
아래의 각 데이터의 의미를 보며 살펴보자
- S = 방문한 노드들의 집합
- d [N] = A → N까지 계산된 최단 거리
-
Q = 방문하지 않은 노드들의 집합
- 확인되지 않은 거리는 전부 초기값을 무한으로 잡는다 ex) INF

-
출발지와 출발지의 거리는 확인해 볼 필요도 없이 당연히 0 값을 가진다는 것을 알 수 있다. 출발지를 A로 설정했기 때문에, d[A]=0이 된다. (A노드를 아직 방문한 것은 아니다.)
-
출발지를 제외한 모든 노드들도 아직 확인되지 않았기에, d[다른 노드]=무한이 된다.
-
Q는 방문하지 않은 노드들의 집합이므로, 초기화할 때는 모든 노드들의 집합이 된다.
-
S는 방문한 노드가 아직 없으므로 공집합 상태이다.
1. 루프를 돌려 이웃 노드를 방문하고 거리를 계산한다.

2. 첫 루프 이후의 그래프의 상태가 업데이트되는 방식

3. 더 빠른 경로를 발견한 경우 ( d[C] = 5->4 ) 값 업데이트

이런 식으로 방문하지 않은 노드 중 비용이 적은 노드를 선택하여 가까운 노드의 비용(그리드 알고리즘)과
해당 노드로부터 갈 수 있는 노드들의 비용을 갱신한다. (다이나믹 프로그래밍)을 반복하여 사용한다.
3.1 더 빠른 경로를 발견한 경우 ( d[E] = 10->6 , d[F] = 11->9) 값 업데이트

E노드에 왔을 때 d[F] = 9 -> 8 값 업데이트

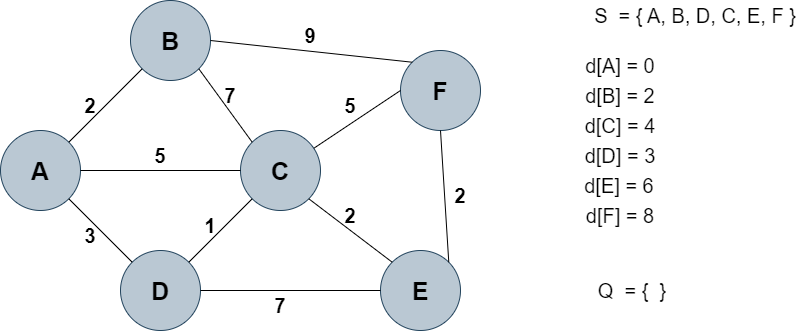
-
d[A] = 0
-
d[B] = 2
-
d[C] = 4
-
d[D] = 3
-
d[E] = 6
-
d[F] = 8
-
Q = ∅
다익스트라 알고리즘 구현방법
다익스트라 알고리즘 : 선형탐색(반복문 이용) O(V^2)
- 한 번 방문한 배열은 방문할 수 없으므로 방문 여부를 체크할 배열이 필요할 것이고, 각 노드 까지의 최소 비용을 저장할 배열이 필요할 것이다.
- 구현에서 고려해 주어야 하는 것은, 미방문 지점의 값을 항상 최소의 값으로 갱신하는 것이 목표이기 때문에, 미 방문 지점은 매우 큰 값으로 초기화하여 처리해주면 된다
- 최소 비용을 갖는 노드을 선택하는 과정은 앞선 일반적인 구현에서는 최악의 경우 모든 노드을 확인해야 하고, 이 것은 V번 반복하기 때문에 O(V^2)의 시간 복잡도를 갖는다
//다익스트라(Dijkstra) 알고리즘
public class Dijkstra_Algorithm {
static int[][] arr;
static boolean[] visit;
static int[] distance;
static int num;
static int max = 10000000;
public static void main(String[] args) {
visit = new boolean[6];
distance = new int[6];
arr = new int[][]{ { 0, 2, 5, 1, max, max },
{ 2, 0, 3, 2, max, max },
{ 5, 3, 0, 3, 1, 5 },
{ 1, 2, 3, 0, 1, max },
{ max, max, 1, 1, 0, 2 },
{ max, max, 5, max, 2, 0 } };
num = arr.length;
dijkstra(0);//1번 노드(index:0)에서 시작하여 각 노드로 가는 최단경로 찾기
for(int i:distance) {
System.out.print(i+" ");
}
}
private static void dijkstra(int start) {
for(int i=0;i<num;i++) {//최초 arr의 값을 distance에 넣어준다
distance[i] = arr[start][i];
}
visit[start] = true;//시작하는 노드를 true로 갱신
for(int i=0;i<num;i++) {
int current = getSmallIndex();
visit[current] = true;
for(int j=0;j<num;j++) {
if(!visit[j]) {
if(distance[current] + arr[current][j] < distance[j]) {//distance[current] : 시작노드(1번노드)에서 current노드로 가는 direct비용
//arr[current][j] : current노드에서 j노드로 가는 direct비용
distance[j] = distance[current] + arr[current][j];
}
}
}
}
}
private static int getSmallIndex() {
int min = max;
int minIndex = 0;
for(int i=0;i<num;i++) {
if(distance[i]<min && !visit[i]) {
min = distance[i];
minIndex = i;
}
}
return minIndex;
}
}
다익스트라 알고리즘 : 우선순위 큐 이용 O((V+E)log V)
- 갱신하는 주변 노드의 값에 대해서만 다음 최소 비용을 갖는 노드를 선택해주면 된다는 것이 우선순위큐를 이용하는 것의 핵심
- 우선순위큐에 추출해주는 연산에대해서는 최대 V개의 노드에 대하여 우선순위큐에서 추출할 것이므로 최대 O(VlogV)의 시간이 걸릴 것이고 따라서 최대 모든 노드, 간선에대하여 우선 순위큐를 계산해줘야 하므로 O((V+E)logV)의 시간이 걸릴 것 이다
- poll() 연산(최소 비용을 뽑는 연산)과 offer() 연산(최소 비용 후보를 우선 순위큐에 넣는 연산)이다. 만일, 중복 노드를 무차별적으로 큐에 넣는다면 위에서 결과적으로 말한 최대 V개의 노드에서 우선순위큐를 추출하는 O(VlogV)가 보장되지 못한다. 따라서, 중복 노드 방문을 두 가지 조건을 기반으로 방지한다.
public class Dijkstra_Algorithm_PriorityQueue {
static int[][] arr;
static boolean[] visit;
static int[] distance;
static int num;
static int max = 10000000;
public static void main(String[] args) {
arr = new int[6][6];
visit = new boolean[6];
distance = new int[6];
arr = new int[][]{ { 0, 2, 5, 1, max, max },
{ 2, 0, 3, 2, max, max },
{ 5, 3, 0, 3, 1, 5 },
{ 1, 2, 3, 0, 1, max },
{ max, max, 1, 1, 0, 2 },
{ max, max, 5, max, 2, 0 } };
num = arr.length;
for(int i=0;i<num;i++) {//우선 distance배열에 모두 최댓값을 삽입
distance[i] = max;
}
dijkstra(0);
for(int i:distance) {
System.out.print(i+" ");
}
System.out.println();
}
public static void dijkstra(int start) {
PriorityQueue<Node3> pq = new PriorityQueue<Node3>();
distance[start] = 0;//자기자신으로 가는 비용으 0
pq.offer(new Node3(start, 0));
while(!pq.isEmpty()) {
int current = pq.peek().index;
int cost = pq.peek().distance;
pq.poll();
if(cost>distance[current]) {
continue;
}
for(int i=0;i<arr.length;i++) {
if(arr[current][i]!=0 && distance[i] > distance[current] + arr[current][i]) {//distance[current] : 시작노드(1번노드)에서 current노드로 가는 direct비용
//arr[current][j] : current노드에서 j노드로 가는 direct비용
distance[i] = distance[current] + arr[current][i];
pq.offer(new Node3(i, distance[i]));
}
}
for(int i:distance) {
System.out.print(i+" ");
}
System.out.println();
}
}
}
class Node3 implements Comparable<Node3>{
public int index;
public int distance;
public Node3(int index, int distance) {
this.index = index;
this.distance = distance;
}
@Override
public int compareTo(Node3 o) {//Node3으로 우선순위 큐를 만들었기 때문에 compareTo메소드를 재정의 해야한다.++
return this.distance - o.distance;//오름차순으로 정렬
}
}
다익스트라 알고리즘 특징
장점
- 인접 행렬 또는 우선순위 대기열을 사용하여 구현할 수 있으므로 가능한 모든 경로를 확인하는 무차별 접근 방식보다 효율적이다.
- 거리뿐만 아니라 경로를 추적하도록 알고리즘을 쉽게 수정할 수 있다.
단점
- 우선순위 대기열을 사용할 때 간선이 많은 큰 그래프의 경우 느려질 수 있다.
- 그래프와 거리를 저장하려면 많은 양의 메모리가 필요하다.
- 동일한 거리에 여러 경로가 있는 경우 최상의 경로를 보장하지 않는다.
- 지형이나 교통 상황과 같은 다른 요소는 고려하지 않는다.
'Back-End > 알고리즘' 카테고리의 다른 글
| [필수 알고리즘] 그리디 알고리즘(Greedy Algorithm) 이해 (0) | 2023.02.03 |
|---|---|
| [필수 알고리즘] 이분 탐색(Binary Search) 이해 (0) | 2023.01.25 |
| [필수 알고리즘] 동적계획법 DP (Dynamic Programming) 이해 (0) | 2023.01.25 |
| [필수 알고리즘] BFS 너비 우선 탐색 (Queue 구조) 이해 (2) | 2023.01.16 |
| [필수 알고리즘] DFS 깊이 우선 탐색 (Stack 구조) 이해 (1) | 2023.01.12 |
![[필수 알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) 이해](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4KlG4%2FbtrZJXczXu4%2F8xyKvYNoI86sTvE6wSile0%2Fimg.png)